(Danh nhân) Fibonacci (khoảng 1170 – khoảng 1250)

Fibonnaci

Leonardo của Pisa (khoảng 1170 – khoảng 1250), còn được biết đến với tên Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, hay, phổ biến nhất, chỉ là Fibonacci, là một nhà toán học người Ý, được một số người xem là "nhà toán học tài ba nhất thời Trung Cổ".

Fibonacci nổi tiếng nhất trong thế giới hiện đại vì:

Có công lan truyền hệ ký số Hindu-Ả Rập ở châu Âu, chủ yếu thông qua việc xuất bản vào đầu thế kỷ 13 trong cuốn Sách tính toán(Liber Abaci) của ông.
Dãy số hiện đại mang tên ông, số Fibobacci, tuy ông không phải là người khám phá nhưng đã dùng nó làm ví dụ trong cuốn Liber Abaci.

Tiểu sử

Leonardo sinh ra ở Pisa. Cha ông, Guglielmo, có biệt danh Bonaccio ("hiền hậu" hoặc "đơn giản"). Mẹ của Leonardo, Alessandra, mất khi ông được chín tuổi. Leonardo sau khi chết được gọi là Fibonacci (lấy từ filius Bonacci, nghĩa là con của Bonaccio).

Guglielmo làm giám đốc một cơ sở thương mại (theo một số người ông làm cố vấn cho Pisa) ở Bugia, một hải cảng ở phía đông Algiers ở vương quốc hồi giáo Almohad ở Bắc Phi (giờ là Bejaia, Algeria). Khi còn là một cậu bé, Leonardo đã đi đến đó để giúp cha mình. Đây là nơi ông đã học hệ ký số Hindu-Ả Rập

Nhận ra rằng số học với chữ số Hindu đơn giản hơn và hiệu quả hơn chữ số La Mã, Fibonacci đã đi du lịch khắp thế giới Địa Trung Hải để học theo những nhà toán học hàng đầu Ả Rập vào thời đó. Leonardo trở về sau chuyến du lịch vào khoảng năm 1200. Vào năm 1202, vào tuổi 32, ông đã phát hành những gì ông học trong Liber Abaci (Sách tính), và từ đó đã giới thiệu chữ số Hindu-Ả Rập cho châu Âu.

Leonardo trở thành vị khách thường xuyên của Hoàng đế Frederick II, người rất thích toán học và khoa học. Vào năm 1240 Cộng hòa Pisa vinh danh Leonardo, được biết đến với tên Leonardo Bigollo,[5] bằng cách trao lương cho ông.

Vào thế kỷ thứ 19, một bức tượng Fibonacci đã được dựng lên ở Pisa. Ngày nay nó nằm ở hành lang của nghĩa trang lịch sử Camposanto ở Piazza dei Miracoli.

Thành tựu

Fibonacci là dãy số kinh điển trong toán học được tìm thấy cách đây hơn 800 năm. Đến nay các nhà khoa học phát hiện nhiều trùng hợp thú vị về dãy số này trong tự nhiên.

Dãy Fibonacci là dãy vô hạn các số tự nhiên bắt đầu bằng 1 và 1, sau đó các số tiếp theo sẽ bằng tổng của 2 số liền trước nó.

Cụ thể, các số đầu tiên của dãy Fibonacci là 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610...

2.1. 2 bài toán thỏ và ong

Leonardo Fibonacci là nhà toán học người Ý, được một số người xem là "nhà toán học tài ba nhất thời Trung cổ". Tên tuổi của ông gắn liền với dãy Fibonacci.

Dãy số Fibonacci công bố vào năm 1202 trong cuốn sách Liber Abacci, được tìm ra qua 2 bài toán kinh điển: bài toán con thỏ và bài toán số "cụ tổ" của một con ong đực.

Bài toán thứ nhất đưa ra giả thiết các đôi thỏ nếu đủ 2 tháng tuổi thì sau mỗi tháng sẽ đẻ được một đôi thỏ con (giả sử các đôi thỏ luôn gồm 2 con đực và cái và không chết). Từ một đôi thỏ sơ sinh ở tháng đầu tiên, Finonnaci muốn tính số thỏ có được ở 1 tháng bất kỳ.

Sau khi thống kê, Fibonacci nhận thấy tháng thứ 1 và tháng 2 chỉ có 1 đôi thỏ. Tháng thứ 3 có 2 đôi, tháng thứ 4 có 3 đôi, tháng 5 có 5 đôi, và cứ thế, số thỏ tháng sau sẽ bằng tổng số thỏ của 2 tháng trước cộng lại.

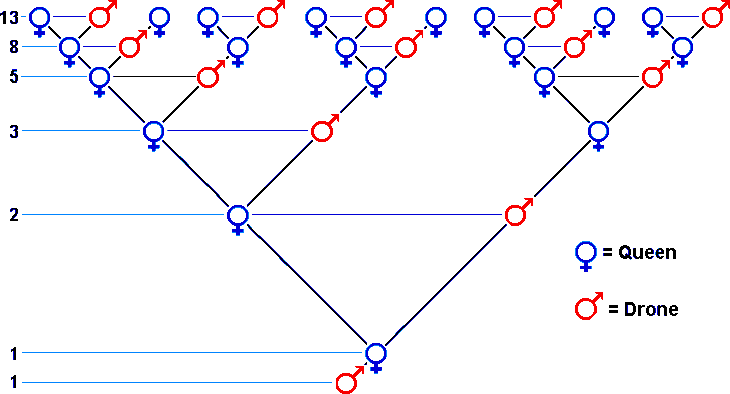
Bài toán thứ hai yêu cầu tìm số tổ tiên của loài ong đực. Nhiều người chỉ biết đến Fibonacci qua bài toán con thỏ, nhưng thật ra còn bài toán về nguồn gốc của ong đực.

Trong sinh học, ong nếu được thụ tinh - tức có cả bố và mẹ, sẽ thành ong cái, ngược lại sẽ là ong đực.

Trong ảnh, màu đỏ là ong đực, màu xanh là ong cái - Ảnh: Dave Cushman

Khi đi tìm nguồn gốc của ong đực, Fibonacci nhận thấy: nếu bắt đầu với 1 con ong đực thì thế hệ trước của nó là 1 con ong cái. Thế hệ trước con ong cái này là 2 con ong gồm 1 đực, 1 cái. Thế hệ trước đó nữa sẽ bao gồm 3 con ong gồm 1 ong cái (sinh ra ong đực) và 2 ong đực và cái (sinh ra ong cái).

Cứ thế tính tiếp tục ta cũng sẽ được dãy 1, 1, 2, 3, 5, 8, 13, 21, 55…

2.2 Quan hệ với tỉ lệ vàng

Trong toán học và nghệ thuật, hai số được coi có tỉ lệ vàng nếu tỉ số giữa tổng 2 số đó với số lớn bằng tỉ số giữa số lớn với số nhỏ.

Khi giải phương trình, ta được tỉ lệ này xấp xỉ 1,61803.

Còn trong dãy Finonacci, tỉ lệ giữa 2 số liên tiếp nhau gần bằng con số này. Ví du: 3/2=1,5; 5/3= 1,66; 8/5= 1,6; 13/8= 1,625… Khi các số trong dãy Finonacci càng lớn thì tỉ số giữa càng gần tỉ lệ vàng.

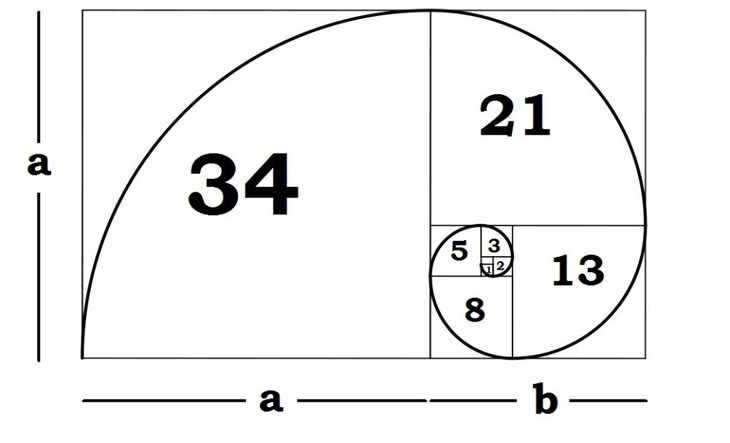
Đường cong biểu diễn tỉ lệ vàng cũng như các dãy số Fibonacci - Ảnh: Livescience

Đây là tỉ lệ được sử dụng rất nhiều trong nghệ thuật vì sẽ tạo ra sự hài hòa và cân đối. Ngoài ra, khi vẽ các hình vuông và hình chữ nhật với độ dài cạnh tương ứng với các số trong dãy Fibonacci và nối các điểm biểu diễn tỉ lệ vàng với nhau ta được đường cong hoàn hảo như trên

2.3 Sự kì diệu trong tự nhiên

Trong tự nhiên có nhiều điều trùng hợp với dãy số Fibonacci hay tỉ lệ vàng.

Hầu hết các bông hoa có số cánh hoa là một trong các số: 3, 5, 8, 13, 21, 34, 55 hoặc 89. Ví dụ: Hoa loa kèn có 3 cánh, hoa mao lương vàng có 5 cánh, hoa cải ô rô thường có 8 cánh, hoa cúc vạn thọ có 13 cánh, hoa cúc tây có 21 cánh, hoa cúc thường có 34, hoặc 55 hoặc 89 cánh.

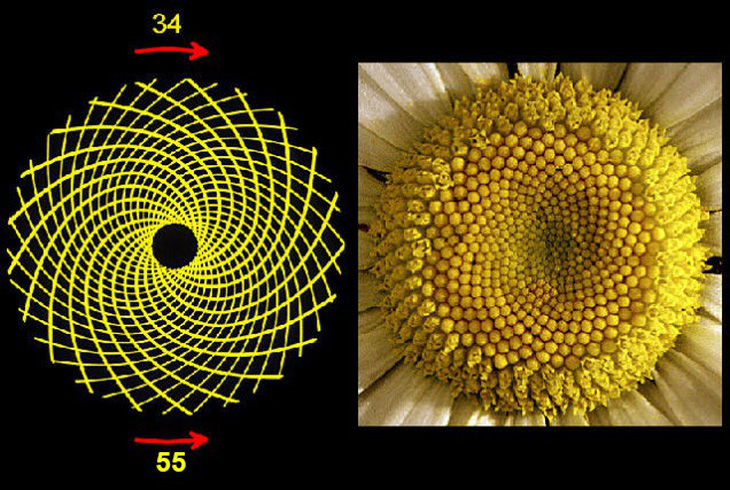
Các số Fibonacci thể hiện trên hoa hướng dương - Ảnh: Slideplayer.com.br

Các số Fibonacci cũng xuất hiện trong bông hoa hướng dương. Cụ thể trong hoa hướng dương, những nụ nhỏ được xếp thành 2 tập hợp các đường xoắn ốc: một tập cuộn theo chiều kim đồng hồ, một ngược theo chiều kim đồng hồ.

Số các đường xoắn ốc hướng thuận chiều kim đồng hồ thường là 34 còn ngược chiều kim đồng hồ là 55. Đôi khi các số này là 55 và 89, và thậm chí là 89 và 144. Tất cả các số này đều là các số Fibonacci kế tiếp nhau.

Số mắt khóm trên những vòng chéo có liên quan đến dãy số Fibonacci - Ảnh: wordpress.com

Nếu quan sát các 'mắt' trên vỏ của một trái khóm chúng ta cũng thường thấy được số mắt trên 2 đường vòng cung chéo trên vỏ trái thơm là 2 số Fibonacci nào đó ví dụ như 13 và 21.

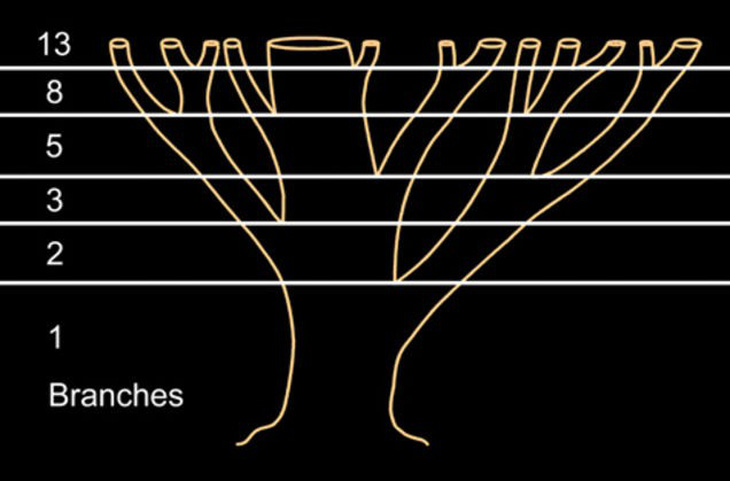
Số nhánh trên một cây - Ảnh: worcester.com.au

Số nhánh của 1 cây từ khi đi từ gốc lên ngọn thường cũng tuân theo dãy Fibonacci khi từ 1 nhánh lên 2 nhánh, 3 nhánh rồi 5, 8, 13 nhánh. Những chiếc lá trên một nhành cây cũng mọc cách nhau những khoảng tương ứng với dãy số Fibonacci.

Ngoài ra còn rất nhiều hình ảnh khác trong tự nhiên có liên quan đến dãy Fibonacci và tỉ lệ vàng.

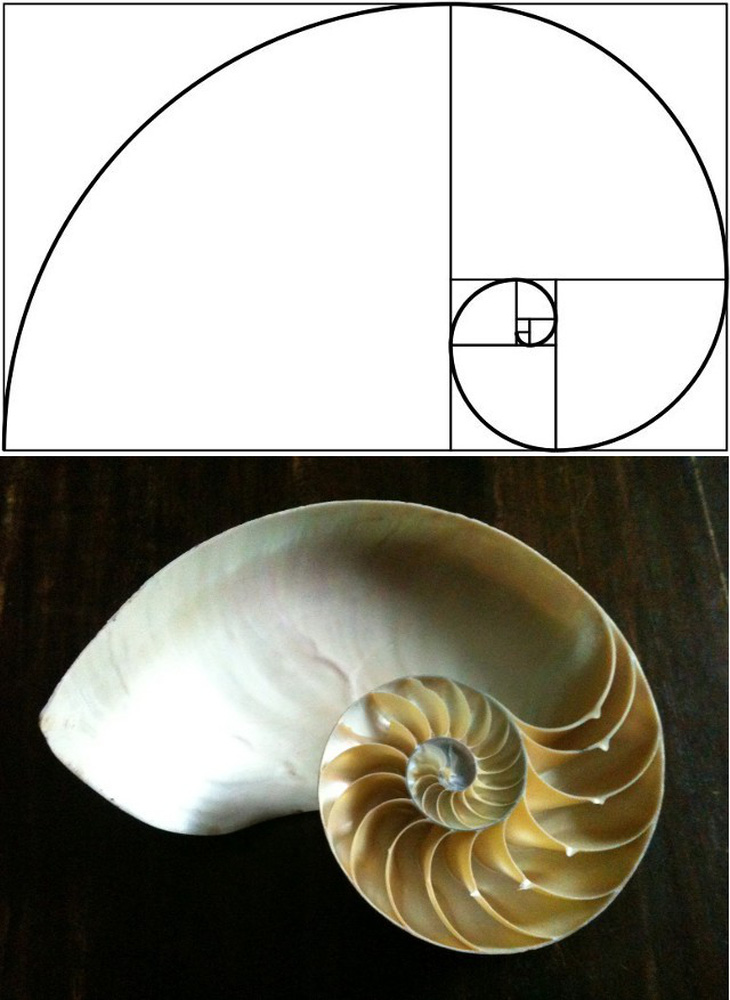
Hình dạng một vỏ ốc giống như đường cong tỉ lệ vàng - Ảnh: Alamy

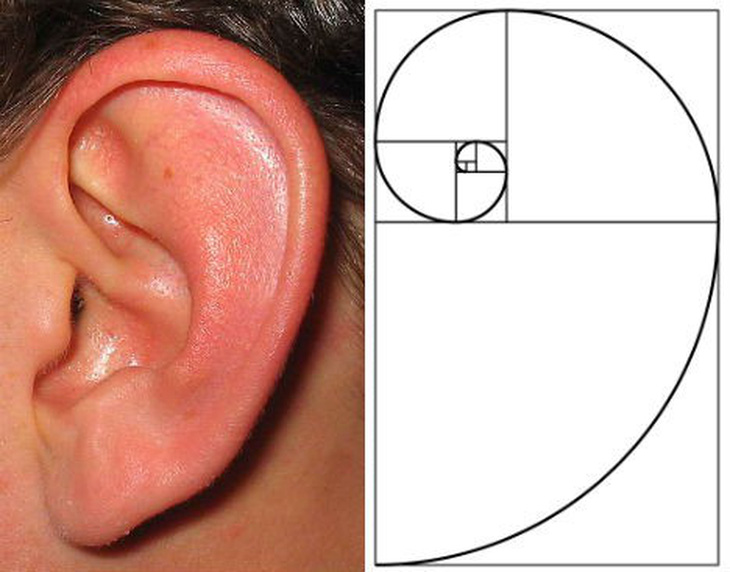
Lỗ tai người và đường cong tỉ lệ vàng - Ảnh: Alamy

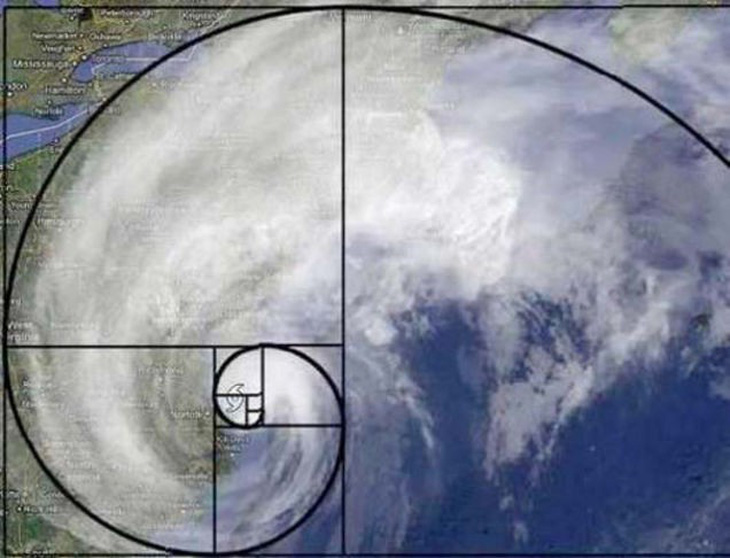
Hình ảnh các cơn bão thường thấy - Ảnh: Getty Images

Tác phẩm

Liber Abaci(1202), một cuốn sách về tính toán
Practica Geometriae(1220), một bản trích yếu về hình học và lượng giác.
Flos(1225), các phép giải bài toán do Johannes của Palermo đưa ra
Liber quadratorum, ("Sách Hình vuông") về phương trình Diophantine, dành tặng cho Hoàng đế Frederick II. Cụ thể xem Đồng nhất thức Fibonacci.
Di minor guisa(về số học thương mại; thất truyền)
Bình luận về cuốn X của Các nguyên tố Euclid(thất truyền)

* Đặc biệt: Tác phẩm Liber Abaci (1202), Fibonacci đã giới thiệu cái gọi là modus Indorum (phương pháp của người Ấn), ngày nay được biết đến với tên chữ số Hindu-Ả Rập (Sigler 2003; Grimm 1973).

Cuốn sách chủ trương dùng phép đếm bằng những con số 0-9 và vị trí của nó trong con số. Cuốn sách để minh chứng tầm quan trọng về thực tiễn của hệ chữ số mới, dùng phép nhân lưới (lattice multiplication) và phân số Ai Cập (Egyptian fractions), bằng cách áp dụng nó vào tính toán sổ sách, chuyển đổi khối lượng và chiều dài, tính toán tiền lời, đổi tiền, và những ứng dụng khác. Cuốn sách được đón nhận rộng rãi khắp giới học giả châu Âu và đã có tác động lớn đến lối suy nghĩa của người châu Âu.

Liber Abaci cũng đề ra, và giải quyết, bài toán liên quan đến sự phát triển dân số giả thuyết của thỏ dựa trên giả thiết lý tưởng. Phép giải, theo từng thế hệ, là một chuỗi các con số sau này được biết với tên Số Fibonacci. Dãy số này đã được các nhà toán học Ấn Độ biết đến từ thế kỷ thứ 6, nhưng nó chỉ đến khi cuốn Liber Abaci của Fibonacci, nó mới được giới thiệu đến phương Tây.

xem thêm nội dung